The Hierarchical navigable small world (HNSW) algorithm is a graph-based approximate nearest neighbor search technique used in many vector databases.
Info
Nearest neighbor search without an index involves computing the distance from the query to each point in the database, which for large datasets is computationally prohibitive.
Info
For high-dimensional data, tree-based exact vector search techniques such as the k-d tree and R-tree do not perform well enough because of the curse of dimensionality.
The HNSW graph offers an approximate k-nearest neighbor search which scales logarithmically even in high-dimensional data.
Probability Skip List
The probability skip list was introduced way back in 1990 by William Pugh. It allows fast search like a sorted array, while using a linked list structure for easy (and fast) insertion of new elements (something that is not possible with sorted arrays).
Skip lists work by building several layers of linked lists. On the first layer, we find links that skip many intermediate nodes/vertices. As we move down the layers, the number of ‘skips’ by each link is decreased.
To search a skip list, we start at the highest layer with the longest ‘skips’ and move along the edges towards the right (below). If we find that the current node ‘key’ is greater than the key we are searching for — we know we have overshot our target, so we move down to previous node in the next level.
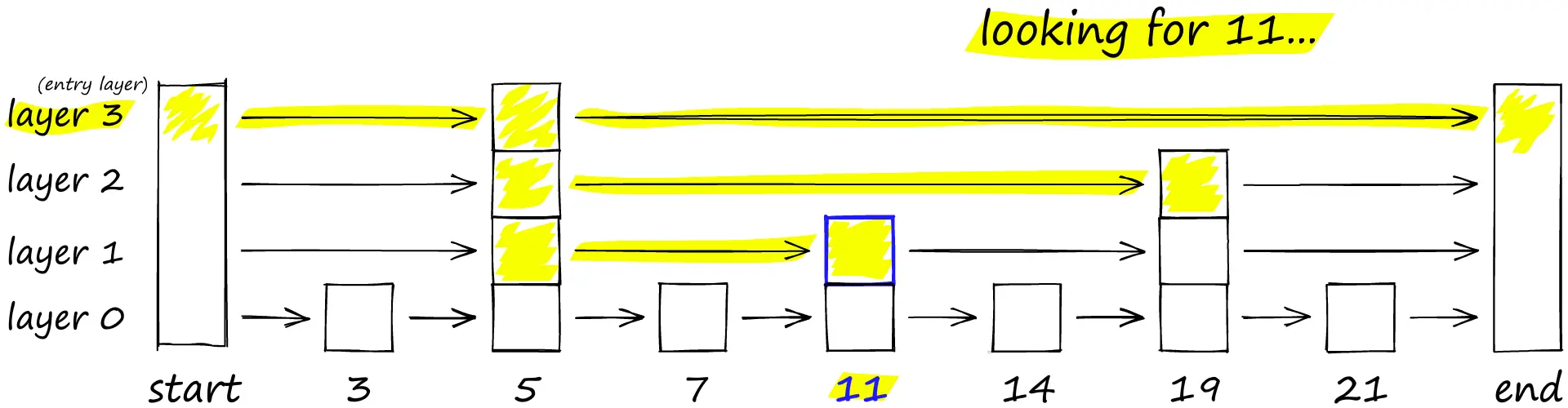 A probability skip list structure, we start on the top layer. If our current key is greater than the key we are searching for (or we reach end), we drop to the next layer.
A probability skip list structure, we start on the top layer. If our current key is greater than the key we are searching for (or we reach end), we drop to the next layer.
HNSW inherits the same layered format with longer edges in the highest layers (for fast search) and shorter edges in the lower layers (for accurate search).